过犹不及，止于至善

Your follow means everything to me, hahaha, thanks!

目录

图的表示方法👉

图卷积的基本表示👉

图的表示方法

一些概念：

节点、边、有向图、无向图、邻接矩阵W；

顶点（节点）的度是所连边的（权重的）和，度矩阵D是对角针，是W的行和；

拉普拉斯矩阵是度矩阵减邻接矩阵(D-W)；

子图A，子图的势

A

等于顶点个数；子图的体积vol(A)等于所有顶点的度之和；

边割：边E的一个子集，去掉边割中所包含的边，图就变成了两个连通子图；

图切割：子图相似度是二者边割的和，也等于子图的切割

最小二分图切割（min「子图的切割」）

以上来自于向世明老师的模式谱聚类的课件

图卷积的基本表示

基本公式：

计算图：

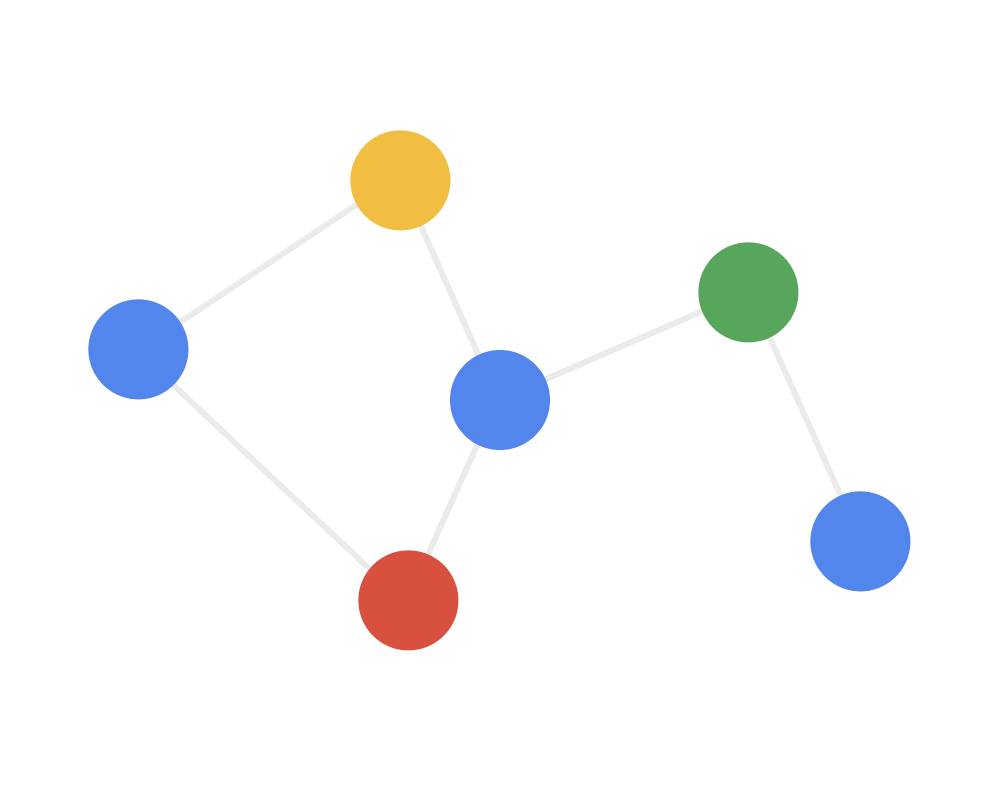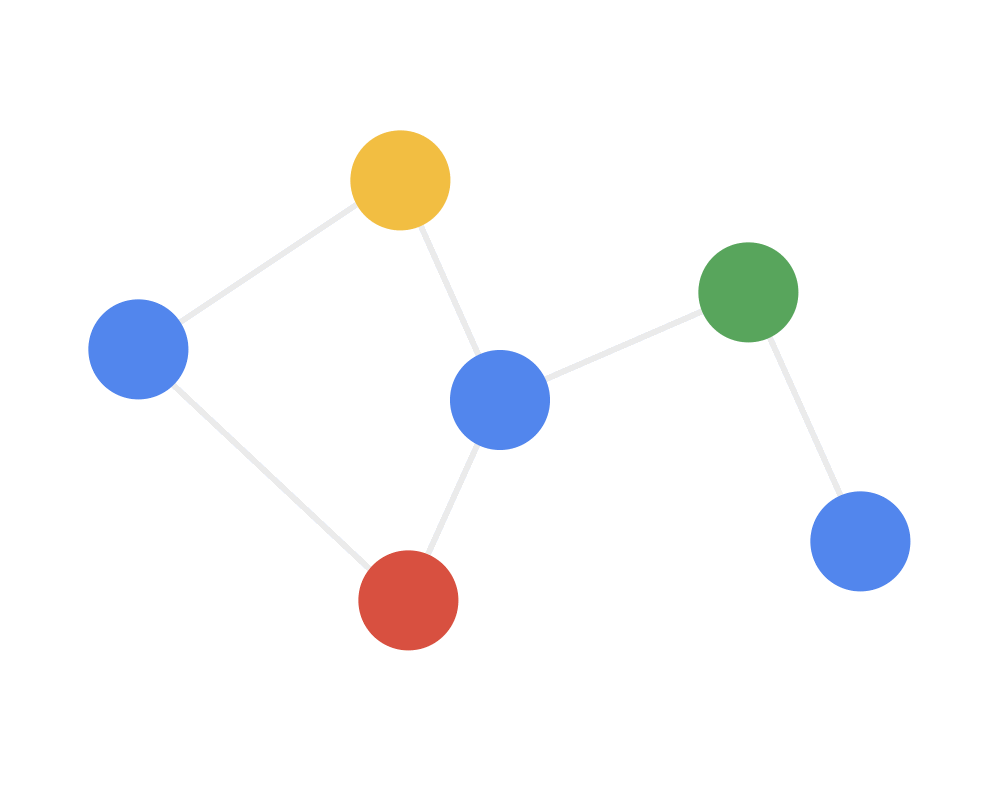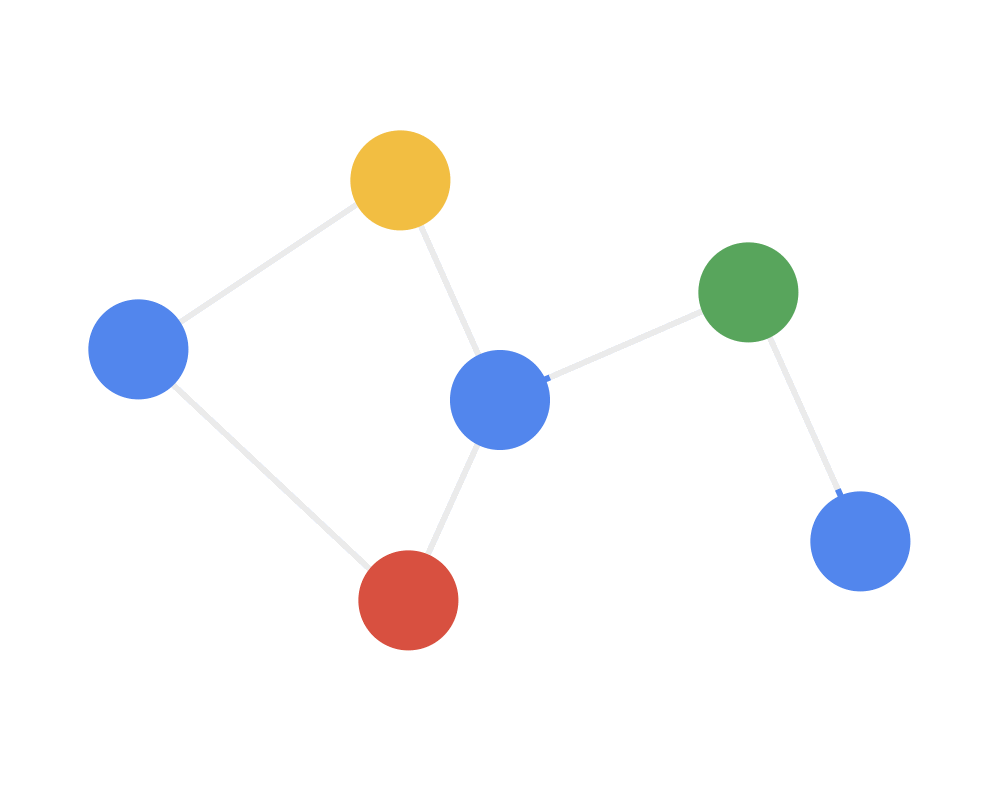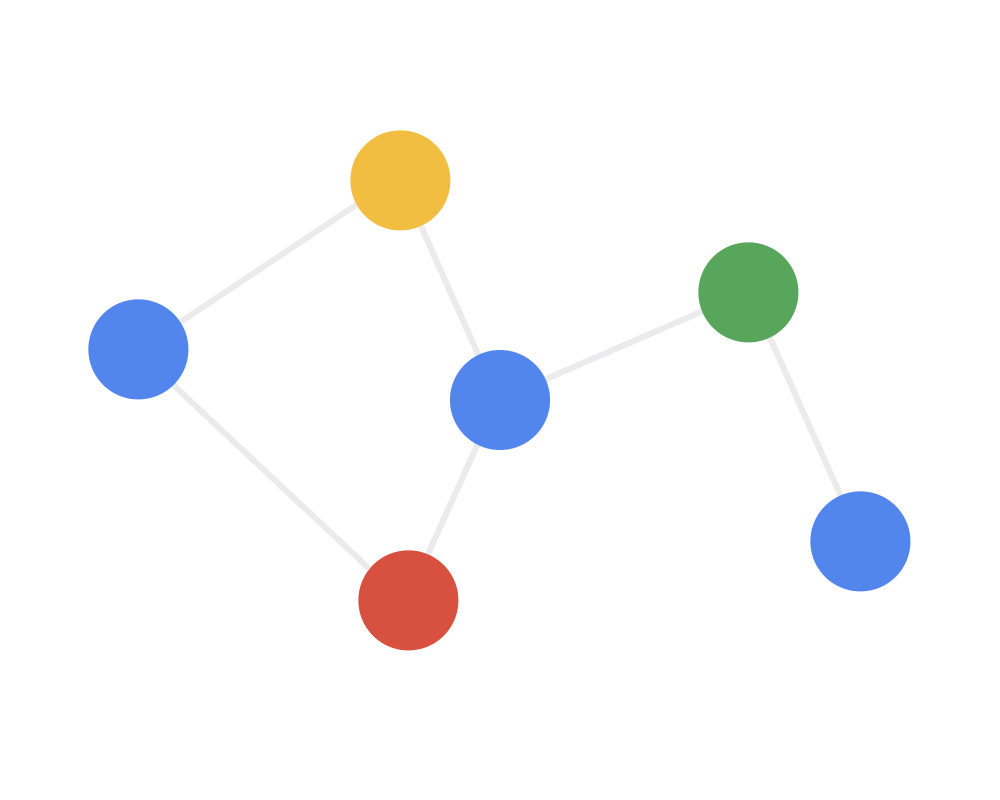
第一步：发射（send）每一个节点将自身的特征信息经过变换后发送给邻居节点。这一步是在对节点的特征信息进行抽取变换。

第二步：接收（receive）每个节点将邻居节点的特征信息聚集起来。这一步是在对节点的局部结构信息进行融合。

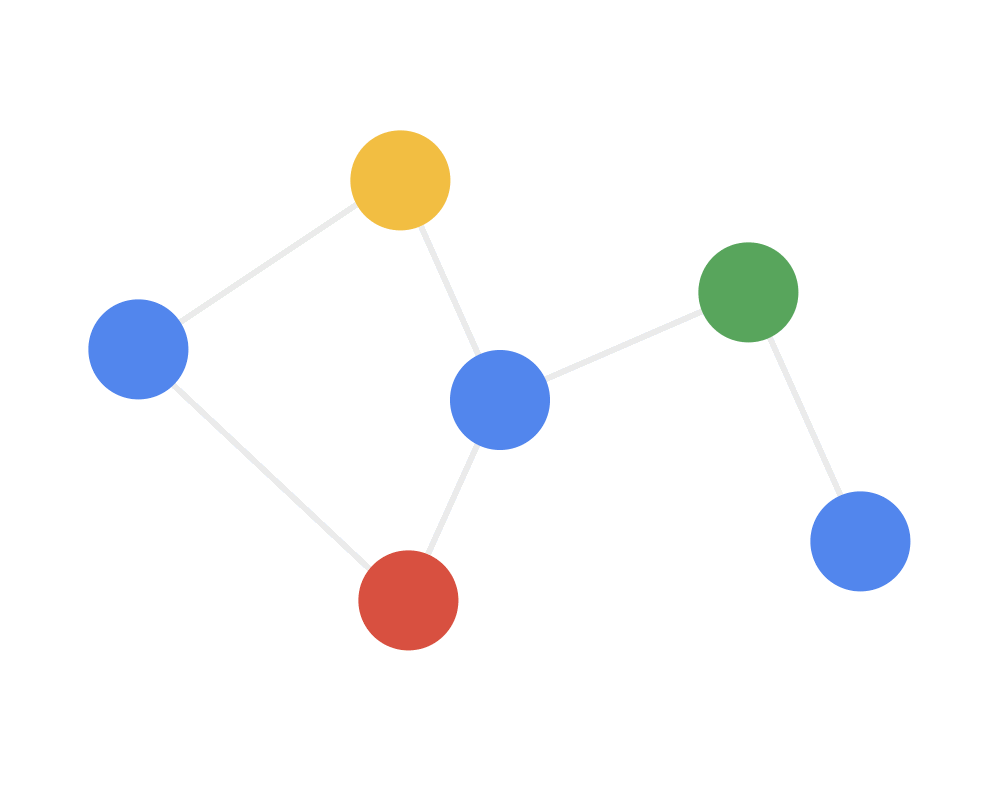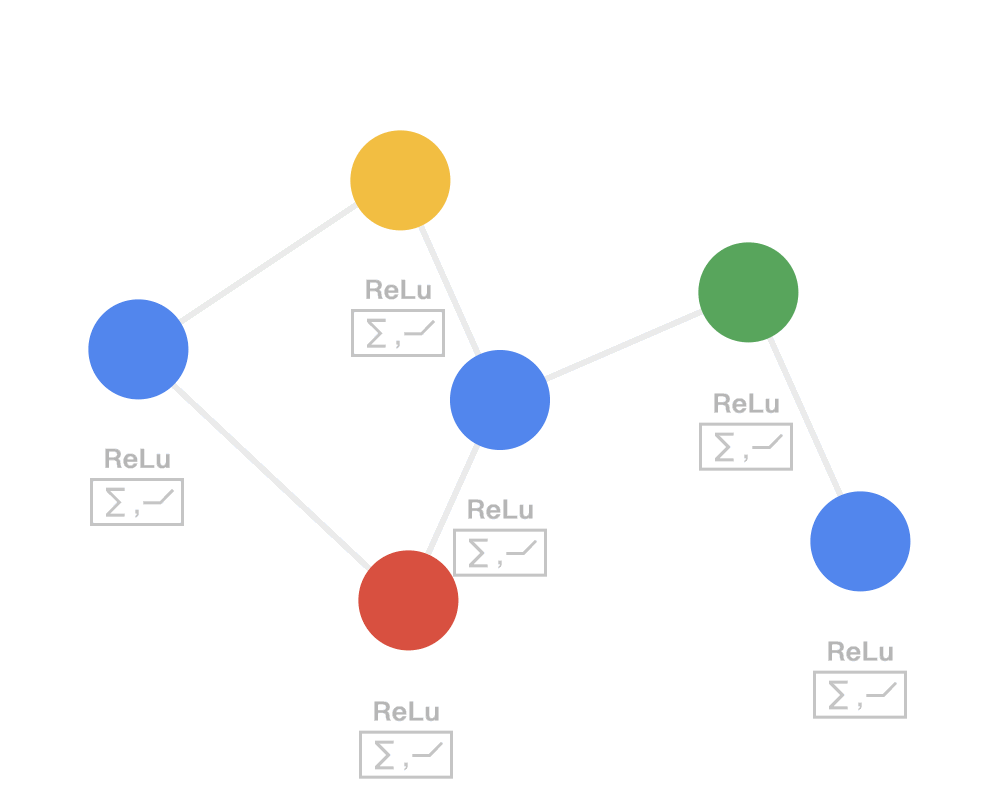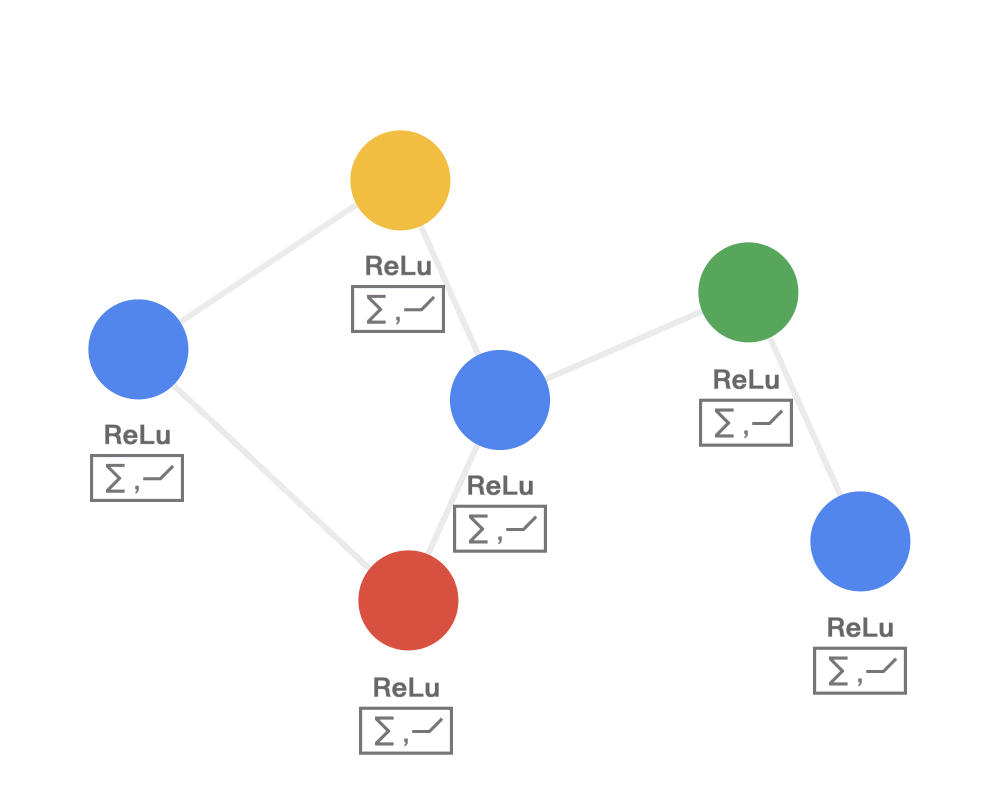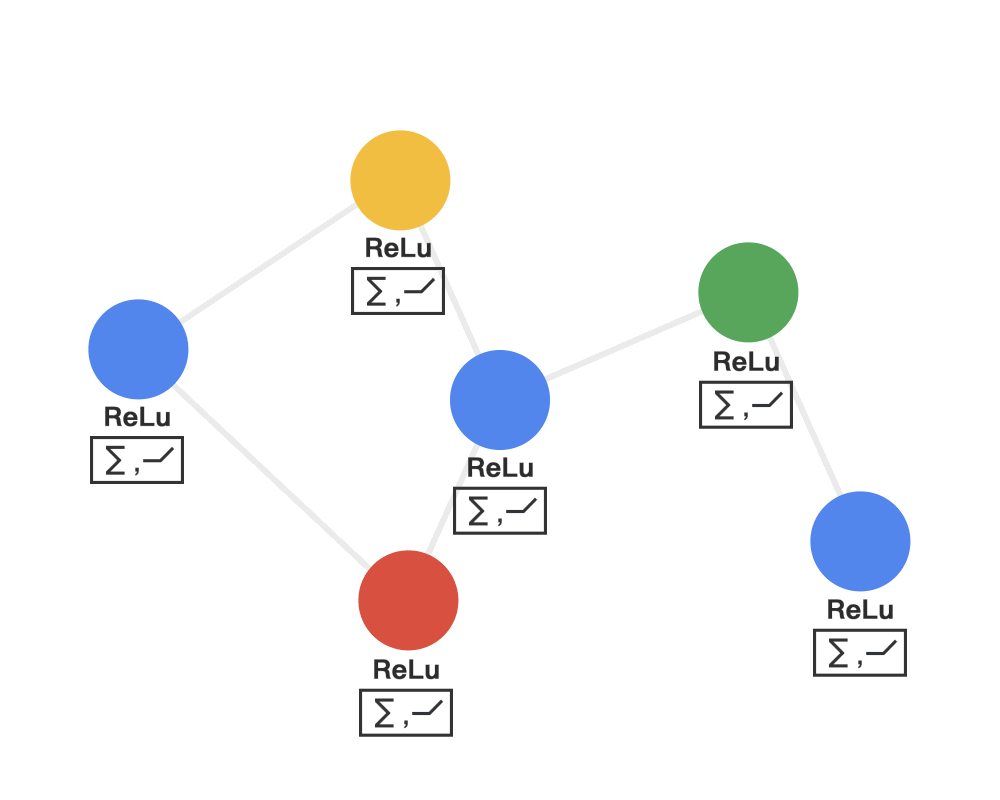
第三步：变换（transform）把前面的信息聚集之后做非线性变换，增加模型的表达能力。

图卷积神经网络具有卷积神经网络的以下性质：

1、局部参数共享，算子是适用于每个节点（圆圈代表算子），处处共享。

2、感受域正比于层数，最开始的时候，每个节点包含了直接邻居的信息，再计算第二层时就能把邻居的邻居的信息包含进来，这样参与运算的信息就更多更充分。层数越多，感受域就更广，参与运算的信息就更多。

GCN的简单框架

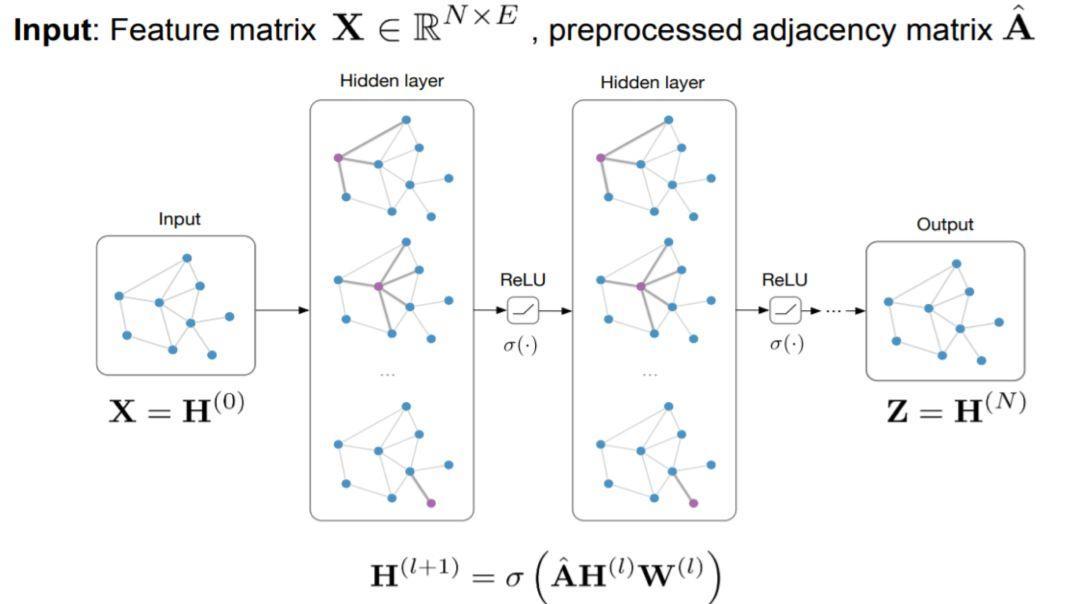
但这也只是在二维平面上进行的操作，如何让GCN有对三维的感知呢？？？